Well, I divided this essay into two parts because the first was getting too long, and now I think the second is twice as long. But that just means it’s twice as interesting. Then the report on the amazing incompetence of Sam Bankman at running FTX came out, and that was topical, so I wanted to publish my comments on that immediately. But I think I must publish this as hot on Bankman’s heels as his creditors because I want to hand it out in class tomorrow to talk about next week. After all, we need to get to Conway’s theorems too. So here’s the rest.
In Part I, I talked about equations both the simple and quadratical, and the Binomial Theorem about which the Major-General was teeming with a lot of news. Now we come to many cheerful facts about the square of the hypotenuse.
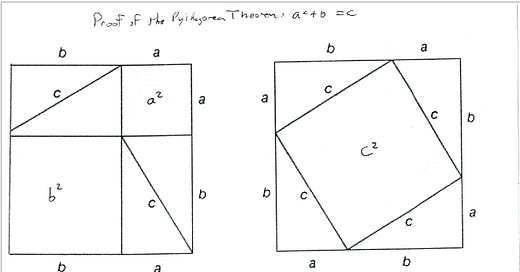
The hypotenuse is the long diagonal side of a right triangle, where a right triangle is any triangle that has a right angle, which is a 90-degree angle. Figure 3 shows an example of a right triangle with sides of length a, b, and c, where c is the length of the long side, the hypotenuse. That’s the triangle you see repeated 8 times there.1

The binomial quadratic expression (x+y)2 relates to how we proved the Pythagorean Theorem in class, which says that the square of the hypotenuse equals the sum of the squares of the other two sides of any right triangle. See Figure 3. The Pythagorean Theorem says that c2 = a2 + b2. That can be proved because in the left panel of Figure 3, (a+b)2 = a2 + b2 + 2ab, as we found in Part I, and ab/2 is the area T of the right triangle the Theorem talks about, but in the right panel (a+b)2 = c2 + 4T. Thus, a2 + b2 + 4T = c2 + 4T, so a2 + b2 = c2 , so we’ve proved the Theorem.2
One student then pointed out that it also came up in another proof we had in class two months ago, the Odd Numbers Squared Minus One Are Divisible by Eight Theorem.
Theorem: Suppose a square's side is an odd number. Then the area of the square minus one is divisible by eight.
Example: Suppose a square’s side is 7 feet long. The area of that square is 49 square feet (7 times 7). Subtract 1, and you 48, which is divisible by 8.
Proof. Let the side of the square have length X. Since X is odd, we can write it as X = 2N+1 for some number N. See Figure 4.
What we must show is that (2N+1)2 -1 is divisible by 8.
Clearly 4N(N+1) is divisible by 4. But we can show that N(N+1) is even (a lemma), so N(N+1) is divisible by 2 and the whole thing is divisible by (4) (2) = 8. The reason the lemma “N(N+1) is even” is true is that either N is even or (N+1) is even, so N(N+1) is an even number multiplied by an odd number. But anything multiplied by an even number is even. So N(N+1) is even, so it is divisible by 2 and 4N(N+1) is divisible by 8. Quod erat demonstrandum.
So much for verse 1 of the Major-General’s Song. That’s most of the math in Pirates of Penzance, except for the calculations that indicate to the noble Frederick “That though you’ve lived twenty-one years, yet, if we go by birthdays, you’re only five and a little bit over!”, the key mathematico-legal idea of the entire opera.
But we do have three more lines of math in The Major-General’s Song:
“I'm very good at integral and differential calculus;
I know the scientific names of beings animalculous:…”
and
“In conics I can floor peculiarities parabolous;”
Integral calculus is about computing the area under curves. Differential calculus is about computing the slope of curves. Consider the equation y = 6x - x2 shown in Figure 5.
If x = 1 then y = 6(1) - (1)(1) = 5. The slope at (1,5) is 4, the same as the slope of the line y = 1 + 4x that goes from (0, 1) to (1, 5) and beyond and which just barely touches the curve. The shaded area under the curve between x = 4 and x = 5 and above the x-axis equals 6 2/3. Calculus got me those numbers using the formulas and calculations below.
If you take calculus, or look around on the Web, you can find out why those formulas are true. They’re half of what you need to know for practical calculus, since you can approximate any function over a finite range by combinations of polynomials like y = xn.
As for parabolas, the Greeks found that you could get the most important shapes of curves—circles, ellipses, parabolas, and hyperbolas— by slicing a cone four different ways. A parabola has an equation like y = 6x - x2; it’s a symmetric hill that rises gently to a highest point and then declines. It is also the shape of the path a ball makes when you throw it and it first rises, then falls under the quadratical pull of gravity. Thus, the curve in Figure 5 is a parabola. Figure 6 shows how all the conic sections are sliced out. The Greeks hadn’t discovered algebra (an Arabic word), so they had to do everything geometrically.
Having read all this, you are now well-equipped for battle, at least so long as the enemy doesn’t use the full-caliber Binomial Theorem against you or ask you tricky calculus questions like “What is the slope of eix? (see the last part of my “(a+b^n)/n = x”. Therefore, God Exists”). Do you think the People’s Liberation Army has it in their arsenal, or are my fears imaginary?3
Speaking of which, if you let a = 1, b = 2, and c = (the square root of 5), you get the Conway Triangle, which I hope to teach soon together with the Conway Circle, the Conway Look-and-Say Sequence, the Conway Expectation Formula, Conway’s Thrackle Conjecture, and maybe even the everywhere discontinous Conway Base-13 Function and Stars over Babylon (his name for the Popcorn Function). Some 21st-century new math discoveries can be taught in middle school (because Euclid could have discovered some of them, but didn’t, which goes to show how smart Conway was till he died of Covid in 2020). Here aer some of the associated figures. (Can you guess which is Stars over Babylon, the Popcorn Function?)
Almost. When famed sports mathematician Jeffrey Sagarin visited my class, he said this proof had bothered him for 60 years (literally). I asked if he’d like someone to explain it; he said yes; and first Kaeb and then Job came up and did the proof on the board. Mr. Sagarin then pointed out which step he found dubious: why in the right panel can we say that the tilted quadrilateral is a square? Each side has length c, to be sure, so it is an equilateral quadrilateral, a rhombus, but to be a square all the angles have to be equal, to be 90 degrees each. So there is a missing lemma to be proved, “Lemma: each angle in the c-sided rhombus is 90 degrees.”
The class took a magical turn then as the class tried to prove the Lemma. Kaeb suggested using the Opposite Angle Theorem somehow. Ruth appealed to symmetry and the fact that the angles of a quadrilateral add up to 360 degrees. Job appealed to symmetry in a different way. One or two other people had ideas. The ideas they proposed all had genuine promise, even if in the time available they ran into dead ends or were just hand waving. I myself tried an idea and failed. We all failed, but these 7th graders were doing Real Math.
At home, I read a bit and then figured out a proof. First, I saw that Wikipedia’s Pythagorean Theorem article slides over the Lemma too. And so does Sir Thomas Heath in his classic 1908 book on Euclid’s Elements (see Vol. I, commentary on Book I Proposition 47, in the 1925 2nd edition, a superb commentary which can be read in isolation from the rest of Heath’s book). But I figured out a proof.
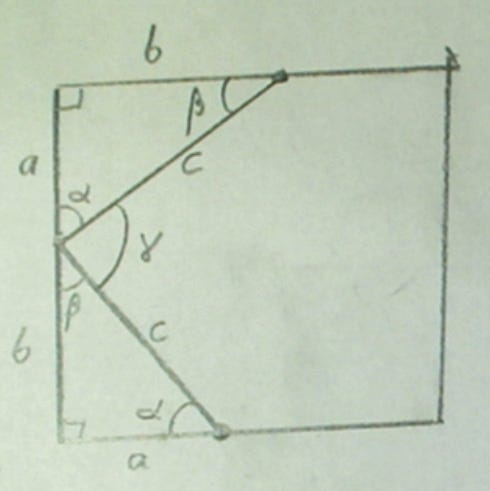
The Pythagorean Lemma: Each angle in the c-sided rhombus in Figure 3 is 90 degrees.
Proof: The Figure below shows half of Figure 3 (which is all we need), with the angles labelled. The triangles are right triangles, so we can label the outer angles as 90 degree angles. The two triangles have exactly the same length sides, so their three angles are the same, so we can label the angles as 90-degrees, α (alpha), and β (beta, pronounced “baytuh”). What we want to know is the size of the angle labelled γ (gamma), which is one of the four angles of the c-sided rhombus.
We know that the three angles of a triangle add up to 180 degrees, so
We can see in the middle of the figure that α plus β plus γ add up to a straight line, so
Thus, γ = 90, quod erat demonstrandum.
A good question is whether the animated video Professor Jay Cummings provides on Twitter is a real proof and subsumes the Pythagorean Lemma. Perhaps I’ll expand all this to a full Substack. I’d like also to talk about whether the Indian and Chinese proofs are really proofs, or just handwaving, since I think they omit the steps. See Heath on this.
There’s some simple notation that would be useful here if you knew it— but hardly any of my readers do, despite it being very common in computer programming. That’s the notation x mod y = z, which means that when you divide x by y, you get a remainder of z. For example, 13 mod 5 = 3, because 13 divided by 5 is 2 with a remainder of 3. You could also say, “Number T is even if and only if T mod 2 = 0”. Thus, the Theorem could be stated:
Theorem: For any odd number n, n2 - 1 mod 8 = 0.
Computer languages have special commands to indicate modulo. In coding with the Python language, for example, you could test whether a number is even this way:
#April 11, 2023. Eric Rasmusen. erasmuse61@gmail.com. #To report bugs.
#This python 3 code tests whether a number is odd and illustrates modulus.
import math as math #This is special package we need for the fmod command.
#First we need to deal with the user interface and get a number to test.
print("What number would you like to test?")
temp1 = input(); #input() asks the viewer to type in.
try: # "Try" and "Except" say what to do if the user makes an error.
temp2 = int(temp1)
#keyboard inputs are always strings,so temp1 must be converted to integer.
except ValueError: #If temp1 isn't convertible, there's an error.
print("It has to be an integer, not a word, even if the word signifies a number, or a decimal.", temp1, "doesn't work. Try again.\n")
temp1 = input(); #Since the first temp1 was bad, try again.
try: #But maybe the user will put in another bad temp1, so let's see.
temp2 = int(temp1)
except ValueError: #If the user does it wrong again, start over.
print("You did it wrong again.", temp1, "doesn't work. Start the program over.\n")
#Next we get to the testing of whether temp1 is odd or even.
answer1 = math.fmod(temp2, 2) #Now we've got to the modulus command, fmod.
if answer1 == 0:
print("The number", temp1, "is even.\n")#Recall that \n means "new line".
else:
print("The number", temp1, "is odd.\n" )
#Now let's do the same test, but with a different python command,
answer2 = temp2 % 2
if answer2 == 0:
temp3 ="The number "+temp1+" is also even using the "+temp1+ " % 2 method."
else: #Python lets you add words, which means to combine them.
temp3 ="The number "+temp1+" is also odd using the "+ temp1 + " % 2 method."
print ("We did that by importing the math module and using the fmod() function, math.fmod(temp,2),but we could have just used temp % 2.\n In Python coding, using modulo is so common it gets to have the percentage symbol dedicated to it\nSo, using %, our answer is still:\n\n", temp3)If you want to have some fun, copy and paste this code into the window at the free online Python app Codabrainy and see what happens.