Why 0.9999 . . . Equals 1.0000 Part 1
When we discussed open and closed intervals in the 7th-grade math class I teach, I stumbled a bit when it came to talking about whether 0.99999 . . . is in the open interval (0,1), which is the set of numbers between 0 and 1 not including the end points. I told the students that for technical reasons we can't say .99 . . . is in the interval, and in fact the convention is that 0.99999 . . . = 1, but it was too hard for me to explain. Job Currell asked his older brother Isaac, though, and found out, and so we talked about it in class. The discussion was good, but I thought I'd better write up a handout to explain the weirdness. It's something I'd never heard of myself until I was in my 50's, when Professor Christopher Connell told me about it. The handout became this Substack article.
Let’s start with the proposition1 at hand:
Theorem 1: 0.999 . . . = 1.
Proof. Let zog1 = 0.3333 . . . define the number zog1. It is then true that zog1 = 1/3. Three times zog1 equals one, because 3 x (1/3) = 1.
Thus, using the 0.3333 . . . way to write zog1, three times zog1 equals 3 x 0.3333 . . . = 1.
But 3 x 0.3333... = 0.999 . . .
Therefore, it must be that 0.999 . . . = 1.
Q.E.D.2
I chose the name zog1 for the variable for 0.999 . . . in honor of Zog I, King of Albania from 1928 to 1939, when Italy conquered his country in World War II. Born Ahmet Muhtar Zogolli, he later changed his name to King Zog. He was a favorite of my college debating club, and, in fact, when we were close to electing a chairman who though a fine fellow lacked humility, we instead elected King Zog and elected him as Acting Chairman.
The key step of the proof is the premise that 0. 333 . . . = 1/3. Given that, ordinary arithmetic gives us 0.999 . . . = 1. When we work with infinity in math we have to be careful because it's not a genuine number--- it's shorthand for "and then keep going with whatever you're doing forever". We don't say that 4/0 equals infinity, we just leave 4/0 undefined, because if we say that 4/0 = infinity, and 5/0 = infinity too, we end up having to say that 4 = 5 if we follow the ordinary rules of arithmetic. We can save arithmetic by saying that 0.999 . . . = 1. It's weird, but that's because we think of 0.999 . . . as a genuine number, but it really is not, since it's built using the idea of infinity. We either have to say that 0.999 . . . is undefined, like 4/0, or let it equal 1, as is done in Theorem 1. What Theorem 1 is doing is assuming implicitly-- that is, assuming without coming out and saying it is making that assumption-- that we want to define and can define 0.999... in such a way that arithmetic works on it.
Mathematicians and math teachers have thought a lot about .999 . . . , as you can see from the Wikipedia article. That article seems to me to make it unnecessarily complicated. I don’t like the Archimidean Principle proofs there that are based on the number line and finding a least upper bound, since I don’t see why making the least upper bound 1 matters to 0.999 . . . , which it seems to me could be *less* than the least upper bound, whereas the argument assumes that it *is* the least upper bound. I think that proof is assuming its answer, by defining 0.999 . . . in a certain way.
Another way to think about it is that 0.999 . . . is just another way to write "1", just as I defined zog1 earlier as another way to write .333 . . . If you think about it as a separate number, you will get all mixed up because there's no way to make it its own number without wrecking arithmetic.
Whichever path you take, we get a good joke.
Question: How many mathematicians does it take to screw in a lightbulb?
Answer: 0.999999 . . .
[This article continues off of Substack at https://rasmusen.org/special/Cedars_School/04.05_3.99999_equals_4.pdf since I need to use a lot of mathematical notation, for which Substack is not well suited but LaTex and pdf are.] [I am writing parts 2 and 3, as of November 2025.]
p.s.: I ought to add this in somehow:
See the excellent and underrated 1662 poem by Michael Wigglesworth, which contains a useful stanza on infinity:
Naught join’d to naught can ne’er make aught,
nor Cyphers make a Sum;
Nor things finite, to infinite
by multiplying come:
A Cockle-shell may serve as well
to lade the Ocean dry
As finite things and reckonings
to bound Eternity.
And talk about .0000001.
And this is not something about using base-10. It works in base 2. 1/3 is .010101 . . .
.99999 is 0.11111110011001100110011 . . . in binary
See https://x.com/IsaacKing314/status/1986147865677406655
If you liked this Substack, you’d like "I Am the Very Model of a Modern Major-General," Part I” and “The Two-Envelope Paradox: Stated but Not Resolved”.
Shortly before revising this in 2025 my high school classmate and computer science professor Andrew Appel pointed out something interesting about propositions. In math (and my field of economics too), a proposition is a true statement, usually with a proof attached. In logic, a proposition is any statement, even one known to be false.
But consider this objection:
My response is that the right-hand-side quantity is never changing. As we add a bit to .333, we subtract a bit from .0001. The number .000 . . . 1 makes no sense. If the zeroes go on forever, you never get to the 1.



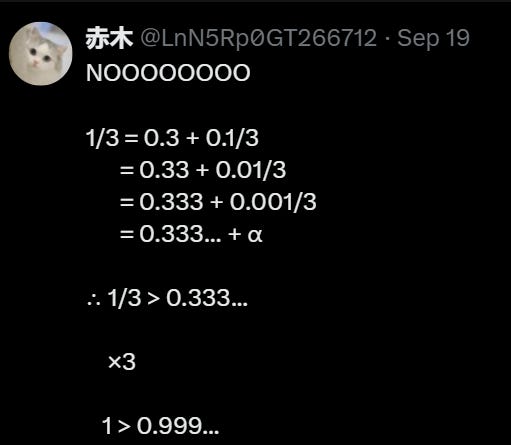
.00000. . . 1=0 or rather makes no sense, because you never get to the 1.
The .3333 + .0003 > 1/3 disproof has the same flaw. You never get to teh 3, or to the 1 in the version I have here.
Axiom: 1/3 = .3333. . . is where the action is. From that we can get .999...=1 and .111... = 1/9, etc.It can be restated that the limit point of a repeating decimal (which is a arational number) equals the repeating decimal.
Base 2--- would it have more problems than base 10, needing more repeating decimals.